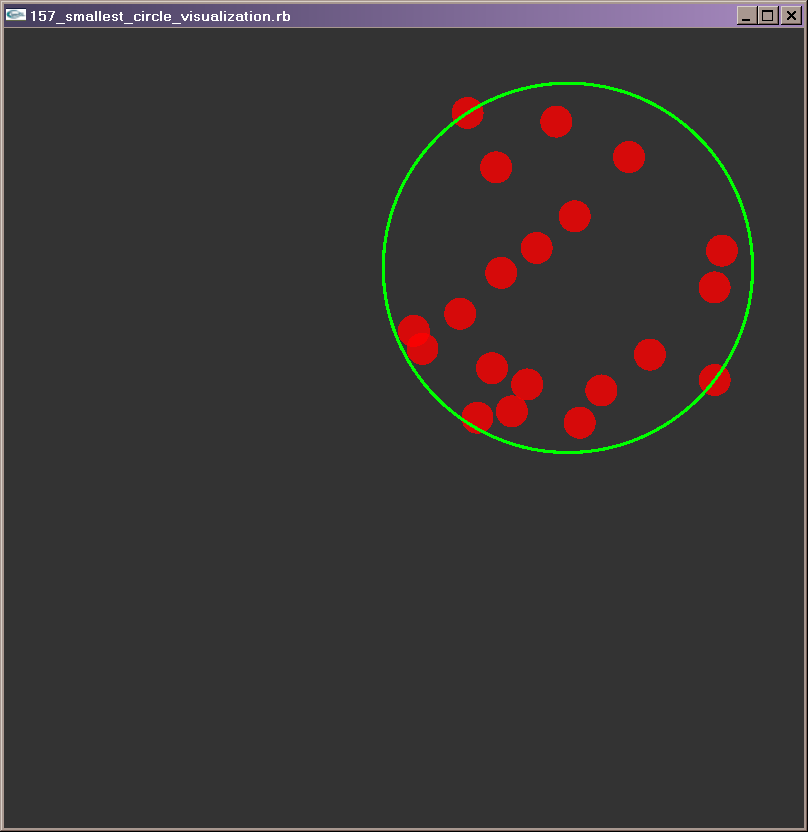
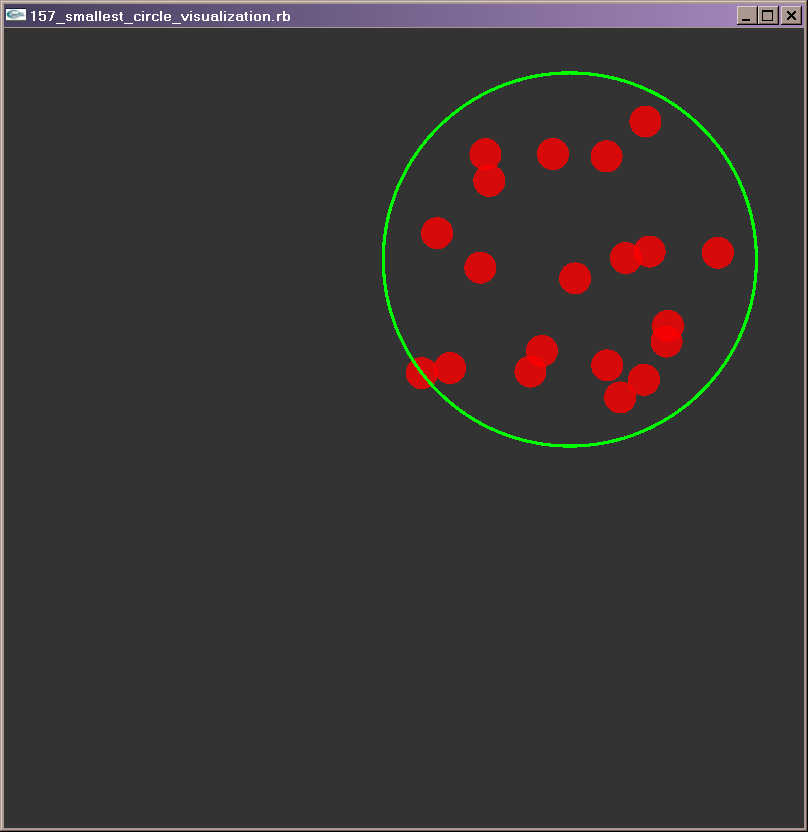
Hi,
here’s my solution. I initially thought that the best circle would be
either defined by a diameter (2 points) or one combinations of 3 points
through which it passes. The idea was that given three points defining a
circle a fourth point is either in the circle or defines a circle with 2
from the 3 originals that includes the remaining point.
This would be neat as I wasn’t so happy about a gradient walking
solution. In this case it can be proven that you can deterministically
get the best solution by gradient walking (I don’t think there are local
maximums) but it’s not the general case. Unfortunately it can be proven
that such a circle can encircle all points, but not that it’s the
smallest (and my experiments proved that it isn’t). Finally this is even
slower than my proposed solution below, …
So here’s a more brute force method : minimizing the maximum distance
with some optimizations (heuristic for initial values and a not so naive
2D-space walker). There’s probably some more optimizations for walking
the gradient but I’m happy with the current speed (~10s for 10000 points
on my 1.06GHz Core Duo).
This seems similar in spirit to Frank’s solution, but less clean from
the Math PoV and more optimized for speed.
It outputs the solution and creates a gnuplot plotting file for you to
verify (you have the path used by the algorithm to find the center). I’m
no Gnuplot expert so unfortunately fancy colors are out and crappy
legends in…
Good reading,
Lionel
=============================================
include Math
Uses 10 points by default
POINT_COUNT = (ARGV[0].to_i == 0) ? 10 : ARGV[0].to_i
class Point < Struct.new(:x, :y)
def self.random
Point.new(rand, rand)
end
def self.generate_samples(n)
(1…n).map { self.random }
end
def to_s
“(#{x}, #{y})”
end
end
class PotentialCenter < Struct.new(:x, :y, :points)
Square distance with a point
def square_distance(point)
((point.x - x) ** 2) + ((point.y - y) ** 2)
end
Maximum square distance with my points
It’s cached because it’s called several times and can be very costly
def max_square_distance
@sq_dist ||= (points.map { |point| square_distance(point) }.max)
end
Compute the best move with given distance (ro)
and angles (thetas)
returns nil if none is better than the current position
def best_move(ro, thetas)
potential_moves = thetas.map { |theta|
new_x = x + (ro * cos(theta))
new_y = y + (ro * sin(theta))
PotentialCenter.new(new_x,new_y,points)
}
choose_move_1(potential_moves)
end
Dumber, faster
def choose_move_1(potential_moves)
potential_moves.detect { |move|
max_square_distance > move.max_square_distance
}
end
Look for the shortest path, slower (~1.4x on average with many
points)
def choose_move_2(potential_moves)
potential_moves.reject! { |move|
max_square_distance <= move.max_square_distance
}
potential_moves.min { |c1,c2|
c1.max_square_distance <=> c2.max_square_distance
}
end
Check that the given offset is big enough to move
the current position
(floating point rounding errors prevent infinite precision…)
def can_be_moved_by(offset)
((x + offset) != x) || ((y + offset) != y)
end
def to_s
“(#{x}, #{y})”
end
end
class Circle < Struct.new(:center, :radius)
def to_s
“{center:#{center}, radius:#{radius}}”
end
end
def chose_original_center_and_move_amount(points)
Start with a good potential (around the middle of the point cloud)
max_x = points.map{|p| p.x}.max
min_x = points.map{|p| p.x}.min
x = (max_x + min_x) / 2
max_y = points.map{|p| p.y}.max
min_y = points.map{|p| p.y}.min
y = (max_y + min_y) / 2
center = PotentialCenter.new(x, y, points)
The original displacement value is based on the fact that a truly
random distribution gets a mean value with a precision of this
order.
The actual center is probably reachable with a few of these steps
move_amount = ((max_y - min_y) + (max_x - min_x)) / points.size
return [center, move_amount]
end
Look for the best center by minimizing
its maximum distance with the given points
This is the same as minimizing its square
(the maximum of the square distances)
This can be seen as a dichotomy on a 2-dimensional space
def encircle(points)
center, ro = chose_original_center_and_move_amount(points)
We’ll move with polar coordinates (distance + angle : ro/theta)
How many directions do we follow?
each new angle creates a new (costly) max_square_distance call
so we take the minimum needed to move around and climb the
square_distance gradient: 3
angle_count = 3
thetas = (1…angle_count).map { |c| (2 * c * Math::PI) / angle_count}
iter = 0
Trace our moves
center_list = []
loop do
center_list << center
iter += 1
puts “#{iter}: #{center.max_square_distance}”
# Is there a best move available ?
if new_center = center.best_move(ro, thetas)
center = new_center
else
ro /= 2
# We stop when ro becomes too small to move the center
break unless center.can_be_moved_by(ro)
end
end
puts “Circle found in #{iter} iterations”
return [ Circle.new(center, sqrt(center.max_square_distance)),
center_list ]
end
points = Point.generate_samples(POINT_COUNT)
t = Time.now
circle, center_list = encircle(points)
puts circle
puts “Found in: #{Time.now - t}s”
Generate a GnuPlot command file to see the result
f = File.open(‘plotcommand.cmd’, ‘w’)
f.print <<EOF
set parametric
set size square
set xrange [-0.2:1.2]
set yrange [-0.2:1.2]
set multiplot
plot “-”
#{points.map { |p| “#{p.x} #{p.y}” }.join("\n")}
end
plot “-” with lines
#{center_list.map { |p| “#{p.x} #{p.y}” }.join("\n")}
end
plot [0:2pi]
(sin(t)#{circle.radius})+#{circle.center.x},(cos(t)*#{circle.radius})+#{circle.center.y}
set nomultiplot
EOF
f.close
puts <<EOF
use ‘gnuplot -persist plotcommand.cmd’ to see
the circle, points and path to the center
EOF