Chuck,
I have a question regarding the comment you made in an earlier email on
the subject:
You said:
Now my question: Is it possible to tune the usrp so the carrier is at
+.31 Mhz ? (band center at 3, from -.2 to 6.2Mhz?) Then we could run
the cpll at 6.4 or 8Msps and get another big performance boost, maybe.
Right now the pll at 19.2 Mhz (6.4 * 3) is an expensive part. Eric, I
guess the bit timing loop would work at 24Mhz (8 * 3).
I don’t see where the 19.2 MHz figure comes about…
My understanding is that when the USRP is tuned to the center of the
6MHz band, the signal that goes through the USB is
u(t) = z(t) exp(-j fsym/4 +j phi)
where fsym = 1/Tsym = 10.76 MHz (so fsym/4=2.69MHz), and
z(t)= x(t)+j x(t) * g(t)
representing the complex lowpass equivalent of the VSB signal.
z(t) is a complex signal with non-zero frequencies in
[-3+2.69,3+2.69]=[-0.31,5.69]MHz
So the signal u(t) needs to be sampled at 6 Complex-Msps, which is what
you do (sampling it at 6.4 Complex-Msps, or as Eric wants at 8
complex-Msps).
Now my understanding is that you need to upsample u(t) by a factor of 2
(in software, ie, making it a 12.8 Complex-Msps signal) and then
run on it the complex pll where the nominal VCO frequency is
fsym/4 = 2.69MHz.
The “out” signal of the cPLL will be the real signal x(t) sampled at
12.8 Msps which is fine since this is the original 8-PAM signal after
Nyquist sampling.
So, what is the 19.2 MHz frequency you are referring to?
The way I see it the cPLL works at 12.8 complex-Msps.
Am I missing something?
Thanks
Achilleas
On Thu, May 22, 2008 at 10:53:12PM -0400, Achilleas A.
wrote:
So the signal u(t) needs to be sampled at 6 Complex-Msps, which is what you
do (sampling it at 6.4 Complex-Msps, or as Eric wants at 8 complex-Msps).
I’m worried about the roll off at the edges of the passband at 6.4 MS/s.
We’re only flat to about 70% of Fs, which is 4.5 MHz at 6.4 MS/s.
If it can be made to work well at 6.4 MS/s, that’s great.
Eric
On Fri, May 23, 2008 at 09:00:31AM -0400, Achilleas A.
wrote:
OK, I see.
- Usually in fractional interpolators the trade-off is: more taps vs finer
sampling. It might be possible to increase the number of taps and still be
able to work with only a 12.8 (or 16) real-Msps.
Having said that, I have to admit I haven’t looked at exactly what this
particular timing loop is doing.
The current resampler requires only 8 taps at each possible fractional
point (1/128). It manages this by having a frequency response that is
unconstrained between Fs/4 and Fs/2. That’s the source of the
constraint on sample rate and occupied bandwidth. The filter design
code is in gnuradio-core/src/gen_interpolator_taps. See the README
there for additional info and references.
We could use a different fractional interpolator, perhaps the one by
Julius O. Smith: http://ccrma-www.stanford.edu/~jos/resample.
With it, 12.8 real-MS/s or 16 real-MS/s should be possible.
Eric
Chuck, Eric,
I think there is a way to perform the cPLL at 8 complex Msps and
upsample to 16Msps only at the very end when you want to get the Real
signal out for further processing. I believe this works (i didn’t see
any point where there is a possibility for aliasing) and it can result
in some savings in complexity without sacrifising performance.
Hopefully I didn’t miss anything big…
Take a look at the block diagram here:
http://www.eecs.umich.edu/~anastas/gnuradio/pll.png
Achilleas
On Thu, 2008-05-22 at 22:53 -0400, Achilleas A. wrote:
Right now the pll at 19.2 Mhz (6.4 * 3) is an expensive part. Eric, I
guess the bit timing loop would work at 24Mhz (8 * 3).
I don’t see where the 19.2 MHz figure comes about…
Nyquist sampling.
So, what is the 19.2 MHz frequency you are referring to?
The way I see it the cPLL works at 12.8 complex-Msps.
Yes, 12.8 or 16Msps would be perfect for the pll - however the next
stage is a ‘bit timing loop’ (atsc.bit_timing_loop) which uses
‘atsci_sssr’ (symbol sync and segment recovery) which uses an
interpolator (gri_mmse_fir_interpolator - ‘minimal mean square error’)
which, for reason unknown to me, requires the
nominal_raio_of_rx_clock_to_symbol_freq (~10.76M) to be greater than
1.8. I relaxed that just a bit to get by with a slightly lower sample
rate of 19.2 (19.2/10.76 ~= 1.7844) which was easy to get from 6.4Msps
which is easy to get from the usrp. It would be nice to be able to
cheaply upsample from 12.8(16) to 19.2(24)Msps somehow. The mmse
interpolator notes says:
- This implements a Mininum Mean Squared Error interpolator with 8
taps.
- It is suitable for signals where the bandwidth of interest B =
1/(4*Ts)
- Where Ts is the time between samples.
That looks like your fsym/4. B = 3.2Mhz at 12.8Msps, and 4.8Mhz at
19.2Msps - I’m not sure what that means  Will the bit_timing_loop
Will the bit_timing_loop
work at 12.8(16)Msps input to recover the 10.76M symbols-per-second?
It’s magic to me.
–Chuck
On Sat, May 24, 2008 at 09:13:13PM -0400, Achilleas A.
wrote:
http://www.eecs.umich.edu/~anastas/gnuradio/pll.png
Achilleas
Thanks!
Eric
On Sat, 2008-05-24 at 21:13 -0400, Achilleas A. wrote:
http://www.eecs.umich.edu/~anastas/gnuradio/pll.png
That is interesting - for what it’s worth, from empirical testing,
Eric’s interpolator actually worked with a rx-clock / symbol rate ratio
of 1.487 = 16 / 10.76, altho with a few more visible errors, and using a
really good signal (a 17 element beam a few hundred yards away from a
100kw transmitter ;).
–Chuck
On Fri, 2008-05-23 at 11:07 -0700, Eric B. wrote:
We could use a different fractional interpolator, perhaps the one by
Julius O. Smith: http://ccrma-www.stanford.edu/~jos/resample.
With it, 12.8 real-MS/s or 16 real-MS/s should be possible.
Ok, I have a working block built on the “secret rabbit code” sample rate
converter ( Secret Rabbit Code (aka libsamplerate) ) library referenced
from the Julius O. Smith site. Have not check performance yet but here’s
a plot of a .8Mhz signal at 16Msps upsampled by 1.487:
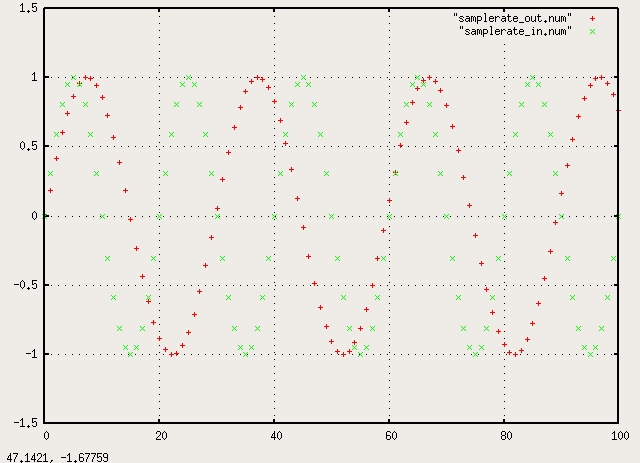
–Chuck
 Will the bit_timing_loop
Will the bit_timing_loop