GNU Radio IIR Filter Taps

GNU Radio
1

Hello,

I’ve been trying to move the fm De-emphasis (an IIR filter, I’m pretty
sure) functionality of the WBFM_Receive block into an FPGA, and I’m a
little confused as to how the taps work.

I’m in fm_emph.py and can see the taps listed as

btaps = [b0, b1]
ataps = [1, a1]

I had assumed this is a first-order IIR filter, and am basing my simple
algorithm on a structure as seen in this link

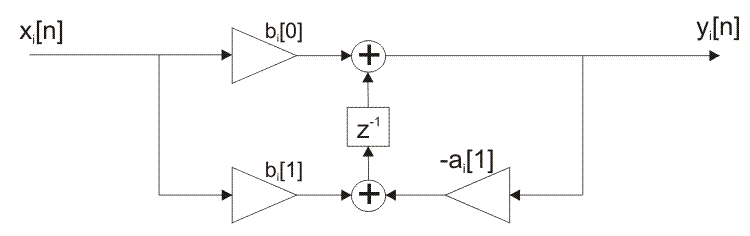
Is there something I’m missing? I don’t seem to be getting the correct
results based off my input data.

Thanks,
Keyur

2

Keyur Parikh [[email protected]] wrote:

I’m in fm_emph.py and can see the taps listed as

btaps = [b0, b1]
ataps = [1, a1]

This looks like “MATLAB form”. If so, the difference equation should be
y(n) = b0x(n) + b1x(n) - a1*y(n-1)

Mark

3

Mark,

Thanks for your reply. Quick question: the second term isn’t b1*x(n-1)?

Keyur

4

Hey, I wanted to post a correction to this for anyone who might come
across
this. I had previously read a discussion from Tom R. and some other
GNU gods discussing the sign of the feedback taps needing to be negated;
when working with the test bench data, that is still the case.

Normally the gain reported from the feedback filters is subtracted, as
in
the equation that Mark posted above. However, when looking at the actual
function in iir_filter.cc it turns out that the feedback coefficients
are
added.

acc = d_fftaps[0] * static_cast<gr_complexd>(input);
for(i = 1; i < n; i ++)
acc += (d_fftaps[i] * static_cast<gr_complexd>(d_prev_input[latest_n +
i]));
for(i = 1; i < m; i ++)
acc += (d_fbtaps[i] * static_cast<gr_complexd>(d_prev_output[latest_m
+
i]));

This means you can either do one of two things when dealing with the
feedback. You can either negate the value of the reported coefficient
when
using it in the equation above, or change the operation of the equation.
Get your taps from fm_emph.py as above, and utilize them in the
following
equation:

y(n) = b0x(n) + b1x(n-1) + a1*y(n-1)

When doing this, the calculated values match what we printed to a file
while under operation.

5

Sorry, you’re right, it should be b1*x(n-1). --Mark